Simple Methods of understanding data (range, variance, standard deviation)
The Problem with the mean
So I have just finished up a post describing the relative merits of the arithmetic mean and it’s beautiful simplicity. Though the arithmetic mean along with any other representation of the central tendency have limits in explaining data to us. Imagine two sets of numbers [-10,0,10,20,30] ==> mean=10 & [8,9,10,11,12] ==> mean = 10. See with these two data sets they have the same mean but the spread (dispersion) of the data is drastically different. So that is why we need to explore additional methods for describing our data. This is where variance comes in, the mean, median are their to give us an indication of the central tendency, but in order to summarise the data properly we need further summary ‘statistics’. I think this is an important point which I find beautiful with stats but I only came to understand later on. We are on a mission to capture the essence of our data by summarizing it. In the same way that a blurb gives an insight to the book, summary statistics gives you an idea of understanding what your data is like without having to look at each piece of it. Fundamental stats is something our brains do intuitively (even if we do it badly by adding our own bias to it), but it is the way we think. When we say the “bus usually arrives between 4.30 & 4.40”, we are describing spread, we are describing the variance of the data.
How to describe spread
The simplest way to look at the spread of the data is to look at the range. This is just taking the max-min, in general when looking at a data set it has little practical use as it does not look at the frequency of the occurrences and is therefore highly influenced by outliers. So practically it may have little use, but it always good to understand the limits of your data, we use it in scenarios when we look at the high/low of a stock price. Also, it provides a good quick way to see if you have outliers in your data which you need to look at.
But a more standard metric of spread is the variance and by transformation the standard deviation.
Variance
The variance is the deviation of every single data point you have away from the mean squared. So in another way it is the average of the squared difference of a point from the mean. The square is there so that we can look at absolute deviations and not be influenced by negative numbers. It is interesting to note when we talk about variance is to link it to how you evaluate predictive statistical models, we look at the errors (which is the deviation of the prediction from the actual value). This is the same as what we are doing with variance where we take a very simple model, predict your data by taking the mean of points and evaluate the deviation. Now variance is denoted by subscript sigma squared (\sigma^2)
Taking the example above: variance_1 = [(-10-10)^2 + (0-10)^2 + (10-10)^2 + (20-10)^2 +(30-10)^2]/5 = 200 variance_2 = [(8-10)^2 + (9-10)^2 + (10-10)^2 + (11-10)^2 +(12-10)^2]/5 = 2
And there is a casing example of using statistic values to explain your data, with the mean they were the same and now with the variance we know that the data in example 1 is greatly more dispersed and as a result we should expect to have values more away from the mean if we take a sample.
Things to think about with variance
Well first off the value of variance is actually in itself quite a weird term, it gives an indication of the spread by its magnitude, but the actual value is not very descriptive. For example estimating bus arrival times, the variance will be described by min^2, which is not very useful for me. This is where the standard deviation will come in. The second thing to think about is the impact of the outliers on the variance, the fact that we square the difference means points which are very far away from the mean will dominate the value of the variance. Try it with the second example if you for some reason had an erroneous point, like someone typing 120 instead of 12 your variance goes to 2400. It is something really important to consider that you need to understand what is the likely spread of your data, and look at methods of removing anomalous points. This is a problem I faced when dealing with large quantities of data inputted by hand, there was a lot of pollution of the data. Finding ways to deal with this is important. Anomaly detection is another topic, you can use statistical models, but also, think about also using physical models where possible. For example in engineering infrastructure physical principles will likely set bounds for your model.
Standard deviation
So the little brother of variance, and most likely the more often used at the day to day level. It is the square root of the variance. \sigma = standard deviation = sqrt(variance)
The standard deviation is nice as it returns the variance into units and a magnitude that we can understand and compare to our data. Also by the fact of its construction (mainly the introduction of a square) it has a lot of nice properties in statistics.
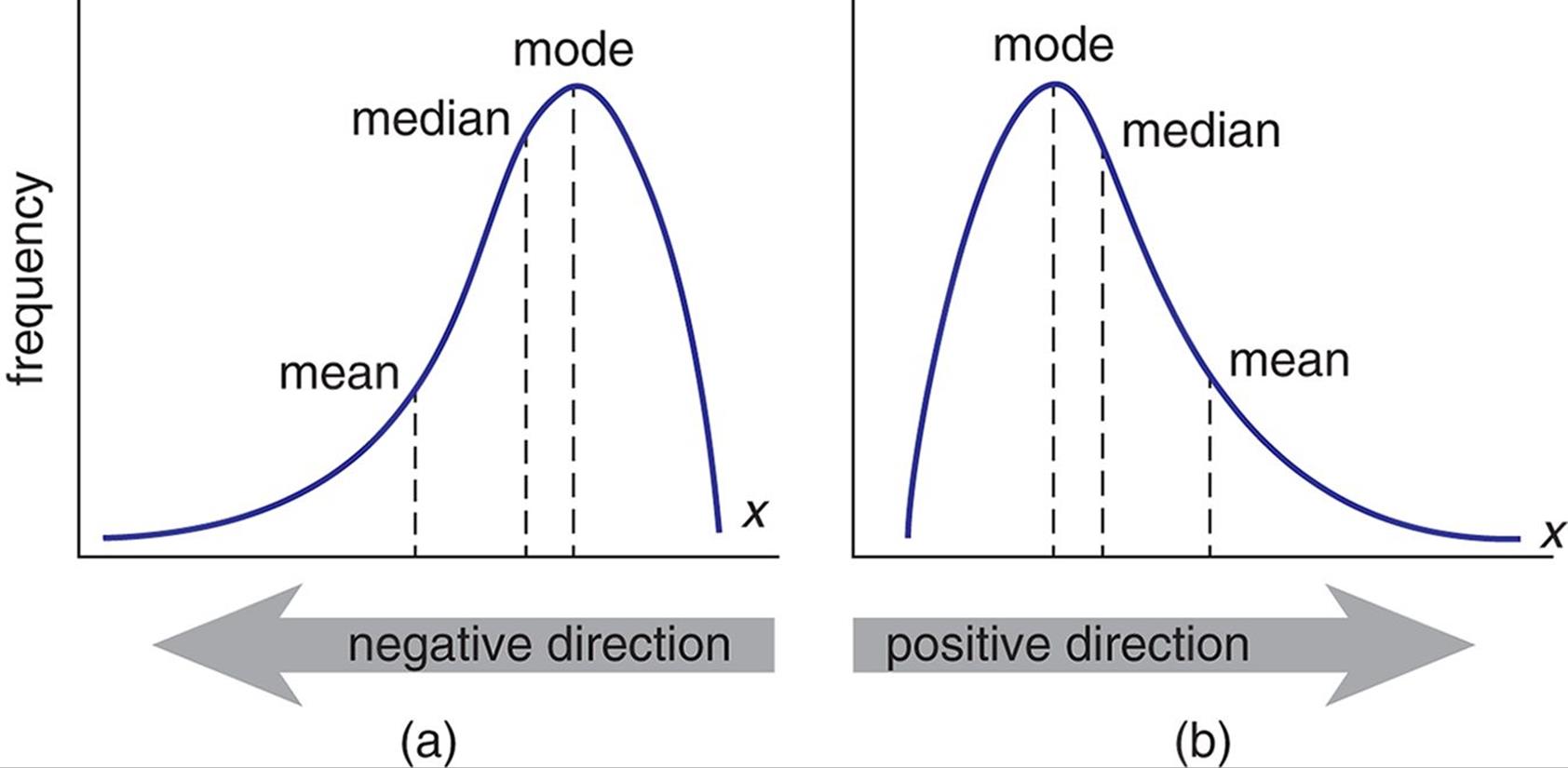
Considerations with Standard Deviation and variance - skewed data
Something to consider and the same goes for both std. deviation and variance. Is that both methods use the mean to calculate the spread of the data. Now that is great if you have normally distributed data (which does happen quite a lot), as the mean is a good representation of the central tendency on the data. However, if the data is heavily skewed (positively or negatively), then the deviation will be hugely impacted by the outliers at one end of the skew. This makes the statistics less useful, when trying to understand the spread of the skewed data it is often better to use the median and inter-quartile range (IQR), as you will be better able to capture the spread around the median both positive and negative.
History of Variance and Standard deviation
Again like many of these recognisable terms there exact origin/inception has many persons t attribute. Though in terms of coining the term variance and its formal definition it was Ronal Fisher (1918), in his paper on population genetics which was submitted to my home town of Edinburgh. Now the general use of a term similar to variance dates back longer than this. Gauss again comes up, in his analysis of the position of stars. He had an issue in that he had many measurements for the position of a single star, but was trying to give its most likely position. He assumed that a star had a fixed position and therefore the measurable points would simply be deviations away from this fixed zero position. These errors were determined by a probability distribution away from the true position of the star. The parameter determining the distribution away from the central tendency was expressed at the time as a parameter called precision. Precision is in fact related to squared deviations which in turn is related to the variance.
References
[1] Khan academy video, https://youtu.be/E4HAYd0QnRc
[2] Image of skewed data, http://schoolbag.info/physics/physics_math/71.html
[3] Earliest Known Uses of Some of the Words of Mathematics, http://jeff560.tripod.com/mathword.html
[4] Why is variance calculated by squaring the deviations?, https://www.researchgate.net/post/Why_is_variance_calculated_by_squaring_the_deviations
