Arithmetic mean - The defacto average - It's past and present
Intro
So this may seem a ridiculously basic blog to write, the arithmetic mean is after all something that we learnt either intuitively or at least at a very young age. But this is part of a series of articles I will write on basic terms and in general statistics. I have been returning over my Maths knowledge and finding many fundamental gaps, I know how to implement it but why I am implementing it, is something I have not been able to answer. I have also taken a somewhat canonical viewpoint to my learning, understanding the history of where the formulas or theories we use come from. I have also had a gripe from how I learnt statistics in formal education and now, what is beautiful about statistics and probability is that the reasons - at least most of the fundamentals - were developed have such direct applicability to day to day life and they were researched and formalized due to very tangible needs.
The Definition
The arithmetic mean is part of a set of three commonly used averaging methods (harmonic and geometric being the others). So it is simply the sum of all the observations divided by the number of observations. In more precise terms it is a description of the central tendency of a set of data. Fundamentally every point is given the same weighting (this is both a positive and negative, which we exploit in distance metrics). Out of harmonic and geometric the arithmetic mean is always the greater one.
Origin
There was no written law saying that we had to average data by the arithmetic mean, it is not some form of fundamental axiom, but it is as natural for us to use it as adding numbers together. There lies its reason to have been formalized, it is so intuitive. It is our method of making sense of all the data signals we have, what time the bus arrives in ‘general’, how many emails I get on an average day… Humans are bad at dealing with lots of data, but summarize all this data into a single value and we are good. Now the need for an average got more formally put when dealing with recording data and like much of early statistics, it benefitted from analyzing space.
So it started a long time go the first written account being with the Babylonians. They were tracking the position the moon, sun and planets and trying to summarize all their different recordings. It is however more traditionally attributed to Hipparchus (190 BC) a Greek astronomer fellow. Though formally defined by Thomas Simpson who presented his formal definition to the Royal society.

Gauss a guy I will obviously be coming back to in later articles on statistics origins said this: “It has been customary certainly to regard as an axiom the hypothesis that if any quantity has been determined by several direct observations, made under the same circumstances and with equal care, the arithmetical mean of the observed values affords the most probable value, if not rigorously, yet very nearly at least, so that is always most safe to adhere to it.”

I like this quote as it comes to a recurring thematic in early research in statistics and like most of mathematics, how do I understand the world around me. This is the core of what I see is in data science and statistical modeling, how do I take all these observations and derive value from them so I can make a better decision or a better prediction. I mean at the simplest level we do this in our head, the bus arrived at 2.15, 2.20, 2.12 what time will it probably arrive today. Telling me a hundred bus times in itself is useless but recombining it into a single number is what makes me able to decide when I leave the house. This is the same objective as we extend, maybe we start to add traffic data, weather data etc. but the idea remains the same as the simple objective that Gauss outlines, “[what value affords the most probable value]”.
What does the arithmetic ‘mean’
Here I mean why is called the arithmetic mean. Well this is because it comes from the notion of an arithmetic series, these are series where each adjacent is a fixed term from the adjacent terms. Now here we get mean by adding up adjacent terms hence arithmetic.
Why is it the biggest mean
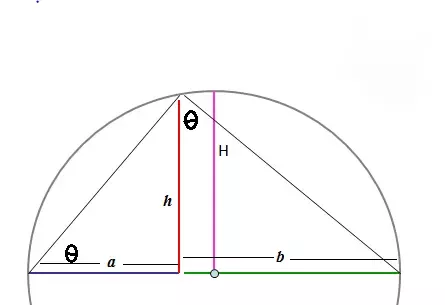
I really liked an explanation on Quora for the reason why the Arithmetic mean is the bigger of the means (a link is provided below, I will paraphrase it here). If we discuss just about two parameters we can look at it through the lens of geometry. If we look at the below circle we see that we have a and b. We also have a chord labelled h which divides a and b. Now the arithmetic average of a & b will always be the radius (a+b = diameter = radius2 ==> radius = (a+b)/2). you can move the chord h and change the size of a+b but they will always sum to the same value.
Now for the geometric mean however you would multiply a & b and take the square root geo_mean = (ab)^0.5. Well lets look at chord h, to calculate the value of h we should recognize that theta the angle adjacent to a is equal to the angle opposite b. From this we see that tan(theta) = h/a & tan(theta) = b/h, bringing this together we see that h^2 = ab ==> h = (ab)^0.5 == geometric mean. Therefore, the geometric mean is represented by the chord h and the arithmetic mean is constant H (the radius). The geometric mean has a maximum value of H, hence the inequality of the geometric <= arithmetic mean. It also shows a nice fact of how the relative size of a and b effect the geometric mean but it is indifferent in the arithmetic mean. This shows a limitation as well, in the case that a could be 0 and b is 6, the average would still be 3, which is not really a representative value for the central tendency of the group. Imagine if this was hourly salary, if one person worked for free and the other earned $6/hr it may be not be representative to say they on average earn 3 dollars.
References
[1] https://www.quora.com/Why-is-the-arithmetic-mean-always-greater-than-or-equal-to-the-geometric-mean [2] http://www.famous-mathematicians.com/hipparchus/
